
 AMS Short Course
AMS Short Course
Discrete Differential Geometry (DDG)
January 8-9, 2018
This two-day course is organized by Keenan Crane, Carnegie Mellon University. The speakers include Yaron Lipman, Weizmann Institute; Justin Solomon, Massachusetts Institute of Technology; Johannes Wallner, TU Graz; and Max Wardetzky, University of Göttingen.
The emerging field of discrete differential geometry (DDG) studies discrete analogs of smooth geometric objects, providing an essential link between analytical descriptions and computation. In recent years it has unearthed a rich variety of new perspectives on applied problems in computational anatomy/biology, computational mechanics, industrial design, computational architecture, and digital geometry processing at large. The basic idea behind discrete differential geometry (DDG) is that a discrete object like a polyhedron is not merely an approximation of a smooth one, but rather a differential-geometric object in its own right. In contrast to traditional discretization which focuses on eliminating approximation error only in the limit of refinement (e.g., by taking smaller and smaller finite differences), DDG places an emphasis on so-called “mimetic” discretization where key properties of a system are guaranteed to be exactly preserved, no matter how fine or coarse the discretization. For instance, just as algorithms for simulating mechanical systems might seek to exactly preserve energy or momentum, structure-preserving discretizations of geometry might seek to exactly preserve quantities like total curvature. More broadly, DDG focuses on the discretization of differential geometric objects that do not naturally fall under the umbrella of traditional numerical analysis. This course provides an overview of recent themes in DDG, including both mathematical developments and examples of how DDG is applied in practice.
Each of the following lectures will provide a self-contained introduction to a core topic in DDG, including necessary review of concepts from the smooth setting, basic principles of discretization, and several instances of real world examples. Each lecture will be broken up into two one hour segments, with the first hour covering theory (both smooth and discrete) and the second hour covering applications. Most of this material will be at a level comparable to an introductory graduate course, similar to the discrete differential geometry course found at brickisland.net/DDGSpring2016. Familiarity with basic PDEs (e.g., heat flow and Laplace’s equation) as well as some basic knowledge of curves and surfaces is useful but not essential.
A “Demo Session” on the first day will allow participants to get some hands-on interaction with the kinds of algorithms discussed in the lectures, allowing them to see how they work?and where they still fail! Interested participants are also invited to bring their own demos to the session.
Lecture Topics
- Discrete Laplace Operators, Max Wardetzky, University of Göttingen
 The Laplace operator is perhaps the most prototypical differential operator for various physical phenomena. It describes, e.g., heat diffusion, wave propagation, steady state fluid flow, and it is key to quantum mechanics.Various of these phenomena call for efficient and reliable computer-based physical simulations. Since computers can only deal with a finite number of pieces of information at a given time, this poses the challenge of how to formulate discrete, finite-dimensional versions of differential operators. This challenge entails both discrete versions of the underlying (often curved) geometry and discrete versions of differential operators, such as the Laplacian, acting on these discrete manifolds. Moreover, for robustness and efficiency, many applications require discrete operators that retain key structural properties inherent in the continuous setting. In this lecture we review some important properties of Laplacians, smooth and discrete. We put special emphasis on a unified framework for Laplacians on Riemannian manifolds alongside discrete Laplacians on graphs and simplicial manifolds by combining perspectives from smooth geometry, discrete geometry, spectral analysis, numerical analysis, and geometry processing. We also discuss important theoretical limitations, namely that discrete Laplacians cannot satisfy all desired properties of the continuous case, such as the maximum principle. Retroactively, this explains the diversity of discrete Laplace operators that to date keep emerging in the literature.
The Laplace operator is perhaps the most prototypical differential operator for various physical phenomena. It describes, e.g., heat diffusion, wave propagation, steady state fluid flow, and it is key to quantum mechanics.Various of these phenomena call for efficient and reliable computer-based physical simulations. Since computers can only deal with a finite number of pieces of information at a given time, this poses the challenge of how to formulate discrete, finite-dimensional versions of differential operators. This challenge entails both discrete versions of the underlying (often curved) geometry and discrete versions of differential operators, such as the Laplacian, acting on these discrete manifolds. Moreover, for robustness and efficiency, many applications require discrete operators that retain key structural properties inherent in the continuous setting. In this lecture we review some important properties of Laplacians, smooth and discrete. We put special emphasis on a unified framework for Laplacians on Riemannian manifolds alongside discrete Laplacians on graphs and simplicial manifolds by combining perspectives from smooth geometry, discrete geometry, spectral analysis, numerical analysis, and geometry processing. We also discuss important theoretical limitations, namely that discrete Laplacians cannot satisfy all desired properties of the continuous case, such as the maximum principle. Retroactively, this explains the diversity of discrete Laplace operators that to date keep emerging in the literature.
- Discrete Parametric Surfaces, Johannes Wallner, TU Graz
 Discrete parametric surfaces are discrete analogues of smooth surfaces. The precise manner of discretization is usually not as straightforward as, say, substituting derivatives by differences. Rather, discretization is guided by the principle that discrete surfaces should exhibit a theory of their own: Discrete minimal surfaces are not only discrete approximations of their smooth counterparts (though they can be), but they are geometric combinatorial objects in their own right. It turns out that there is a rich theory of discrete surfaces which is related to discrete integrable systems. It can even be seen as a master theory containing the smooth case as a limit, and which is capable of painlessly explaining certain phenomena exhibited by smooth surfaces that otherwise would not have a systematic explanation. On the application side, this field recently attracted interest from an unexpected source, in connection with freeform architectural designs and the question how to actually build them.
Discrete parametric surfaces are discrete analogues of smooth surfaces. The precise manner of discretization is usually not as straightforward as, say, substituting derivatives by differences. Rather, discretization is guided by the principle that discrete surfaces should exhibit a theory of their own: Discrete minimal surfaces are not only discrete approximations of their smooth counterparts (though they can be), but they are geometric combinatorial objects in their own right. It turns out that there is a rich theory of discrete surfaces which is related to discrete integrable systems. It can even be seen as a master theory containing the smooth case as a limit, and which is capable of painlessly explaining certain phenomena exhibited by smooth surfaces that otherwise would not have a systematic explanation. On the application side, this field recently attracted interest from an unexpected source, in connection with freeform architectural designs and the question how to actually build them.
- Discrete Mappings, Yaron Lipman, Weizmann Institute
 Piecewise-linear triangle meshes are widely popular for surface representation in the digital computer; mappings of meshes are therefore central for applications such as computing good coordinate systems on surfaces (parameterization), finding correspondence between shapes, and physical simulation. However, representation and calculation of mappings in a computer pose several challenges: (i) how to define faithful discrete analogs of properties of smooth mappings (e.g., angle or area preservation), (ii) how to guarantee properties such as injectivity and/or surjectivity, and (iii) how to construct mappings between non-Euclidean (curved) domains.
Piecewise-linear triangle meshes are widely popular for surface representation in the digital computer; mappings of meshes are therefore central for applications such as computing good coordinate systems on surfaces (parameterization), finding correspondence between shapes, and physical simulation. However, representation and calculation of mappings in a computer pose several challenges: (i) how to define faithful discrete analogs of properties of smooth mappings (e.g., angle or area preservation), (ii) how to guarantee properties such as injectivity and/or surjectivity, and (iii) how to construct mappings between non-Euclidean (curved) domains.- One particularly interesting sub-class of simplicial mappings is the collection of convex combination mappings [1, 2] where the image of each vertex of the triangulation is restricted to the convex-hull of its immediate neighbors’ images. Convex combination mappings can guarantee injectivity, are simple to compute algorithmically, offer a discrete analog to harmonic mappings, and can be used to approximate conformal mappings.
- This lecture provides an introduction to convex combination mappings, their generalizations, as well as algorithmic aspects and practical applications.
- Discrete Conformal Geometry, Keenan Crane, Carnegie Mellon University
 Angle-preserving or conformal mappings are a central object in complex analysis and surface theory; they have also proven to be an essential component of a broad range of numerical algorithms including surface meshing, comparative data analysis, physical simulation, and computational design. Why such great interest in maps that preserve angle? One reason is that, computationally, problems involving conformal maps often reduce to solving easy linear problems, allowing algorithms to scale to many millions of degrees of freedom, or providing an effective starting point for more difficult nonlinear problems. Another is that angle preservation is directly linked to real mechanical or constitutive properties of physical systems, where other types of mappings are simply not appropriate.
Angle-preserving or conformal mappings are a central object in complex analysis and surface theory; they have also proven to be an essential component of a broad range of numerical algorithms including surface meshing, comparative data analysis, physical simulation, and computational design. Why such great interest in maps that preserve angle? One reason is that, computationally, problems involving conformal maps often reduce to solving easy linear problems, allowing algorithms to scale to many millions of degrees of freedom, or providing an effective starting point for more difficult nonlinear problems. Another is that angle preservation is directly linked to real mechanical or constitutive properties of physical systems, where other types of mappings are simply not appropriate.- This lecture gives a broad introduction to smooth conformal geometry and discrete algorithms. The richness of the discrete question arises from the many different possible characterizations of conformal maps in the smooth setting: beyond preservation of basic quantities like angles or lengths, conformal maps can be obtained via solutions to elliptic PDEs like Cauchy?Riemann, or parabolic flows like Yamabe or Ricci flow (to name just a few). Although these descriptions are all essentially equivalent in the smooth setting, each perspective can lead to very different ideas about discretization, which in turn provide different algorithmic guarantees. Specific topics include Thurston’s circle packing conjecture, algorithms for circle packing/circle patterns, discrete complex analysis on integer grids and quad graphs, discrete Yamabe flow and its relationship to length cross ratios, as well as recent developments on a discrete theory for surfaces immersed in in $\mathbb{R}^3$. We will touch on applications in geometry processing including surface parameterization, landmark correspondence, surface deformation, and metric reconstruction.
- Optimal Transportation on Discrete Domains, Justin Solomon, Massachusetts Institute of Technology
 Inspired by the matching of supply to demand in logistical problems, the optimal transportation (or Monge?Kantorovich) problem involves the matching of probability distributions defined over a geometric domain such as a surface or manifold. After discretization, optimal transportation becomes a large-scale linear program, which typically is infeasible to solve efficiently on triangle meshes, graphs, point clouds, and other domains encountered in graphics and machine learning. Recent breakthroughs in numerical optimal transportation enable scalability to orders-of-magnitude larger problems, solvable in a fraction of a second.
Inspired by the matching of supply to demand in logistical problems, the optimal transportation (or Monge?Kantorovich) problem involves the matching of probability distributions defined over a geometric domain such as a surface or manifold. After discretization, optimal transportation becomes a large-scale linear program, which typically is infeasible to solve efficiently on triangle meshes, graphs, point clouds, and other domains encountered in graphics and machine learning. Recent breakthroughs in numerical optimal transportation enable scalability to orders-of-magnitude larger problems, solvable in a fraction of a second.- In this lecture, we will discuss advances in numerical optimal transport that leverage understanding of both discrete and smooth aspects of the problem. State-of-the-art techniques in discrete optimal transportation combine insight from partial differential equations (PDE) with convex analysis to reformulate, discretize, and optimize transportation problems. The end result is a set of theoretically-justified models suitable for domains with thousands or millions of vertices. Since numerical optimal transport is a relatively new discipline, special emphasis will be placed on identifying and explaining open problems in need of mathematical insight and additional research.
Image Credits
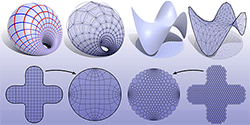
Header image courtesy of Keenan Crane and Max Wardetzky.
Headshot of Max Wardetzky courtesy of Max Wardetzky.
Headshot of Yaron Lipman courtesy of Yaron Lipman
Headshot of Johannes Wallner © TU Graz.
Headshot of Kennan Crane by James Tsui.
Headshot of Justin Solomon by Lillie Paquette/MIT School of Engineering.
References
[1] W.T. TUTTE, How to Draw a Graph, P. Lond. Math. Soc., 13 (1963), 743?767.
[2] MICHAEL S. FLOATER, One-to-One Piecewise Mappings Over Triangulations, Math. Comput., 72 (October 2002), 685?696.